Tam giác đồng dạng là một kiến thức cơ bản và vô cùng quan trọng trong chương trình toán lớp 8 ở bậc THCS. Vậy khái niệm, tính chất, cách chứng minh hai tam giác đồng dạng với nhau như thế nào? Hãy cùng theo dõi lời giải đáp của thegioimay.org qua bài viết dưới đây nhé!
Nội dung chính
Tìm hiểu khái niệm 2 tam giác đồng dạng?
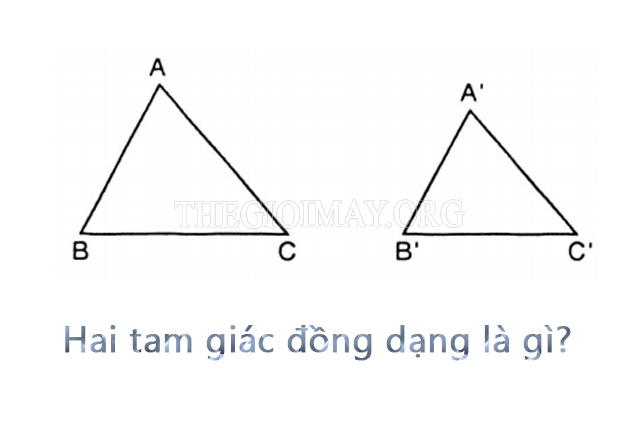
Theo khái niệm của sách giáo khoa toán 8 thì hai tam giác được coi là đồng dạng với nhau nếu chúng có ba cặp góc từng đôi một bằng nhau và ba cặp cạnh tương ứng tỉ lệ. Phép đồng dạng có kí hiệu là: ∼
Có những trường hợp nào của 2 tam giác đồng dạng?
Ở mỗi loại tam giác thường và tam giác vuông, chúng ta đều có tất cả 3 trường hợp tam giác đồng dạng.
Trường hợp đồng dạng trong tam giác thường
*Trường hợp đồng dạng 1: Cạnh – cạnh – cạnh
Nếu hai tam giác có ba cặp cạnh tương ứng bằng nhau thì hai tam giác đó được coi là đồng dạng với nhau. Ví dụ được biểu diễn minh họa qua hình vẽ:
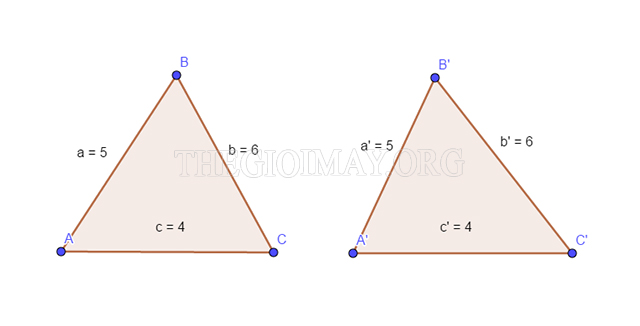
Chứng minh: – Xét hai tam giác ABC và tam giác A’B’C’, ta có:
AB=A’B’=5cm
BC=B’C’=6cm
AC=A’C’=4cm
-> ∆ABC ∼ ∆A’B’C’ (dpcm – Điều phải chứng minh)
*Trường hợp đồng dạng 2: Góc – góc
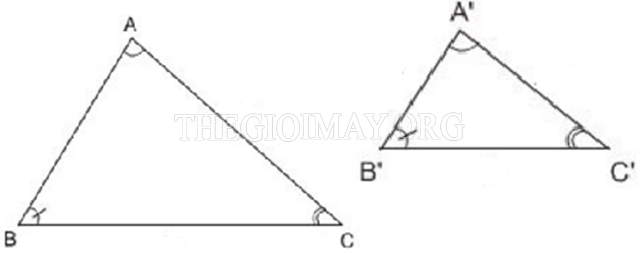
Nếu hai tam giác có một trong hai cặp góc tương ứng bằng nhau thì được gọi là đồng dạng với nhau.
Chứng minh: Xét hai tam giác ABC và tam giác A’B’C’, ta có:
Góc A = Góc A’
Góc B = Góc B’
> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng 3: Góc – cạnh – góc
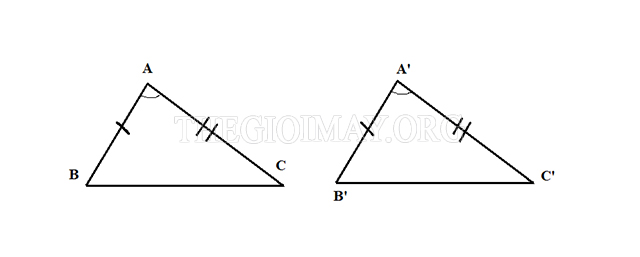
Nếu hai tam giác có hai cặp cạnh tương ứng tỉ lệ với nhau và một góc xen giữa hai cặp cạnh đó bằng nhau thì chúng được gọi là hai tam giác đồng dạng.
Chứng minh: Xét hai tam giác ABC và tam giác A’B’C’, ta có:
AB/A’B’ = AC/A’C’
Góc A = Góc A’
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
Trường hợp đồng dạng trong tam giác vuông là gì?
*Trường hợp đồng dạng 1: Cạnh huyền – cạnh góc vuông
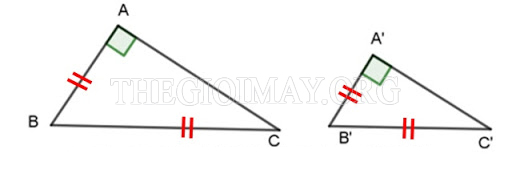
Nếu tam giác vuông này có cặp cạnh huyền và cạnh góc vuông tỷ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
AB/A’B’= BC/B’C’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng 2: Hai cặp cạnh góc vuông
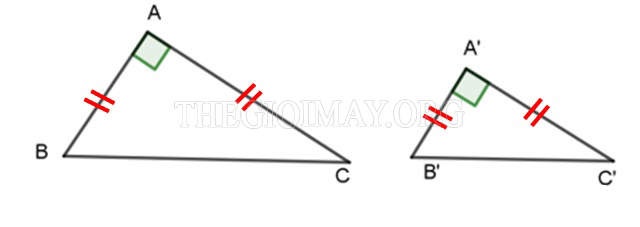
Nếu hai tam giác vuông có hai cặp cạnh góc vuông tỷ lệ với nhau thì hai tam giác đó được gọi là đồng dạng với nhau.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
AB/A’B’= AC/A’C’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
*Trường hợp đồng dạng thứ 3: Góc – góc
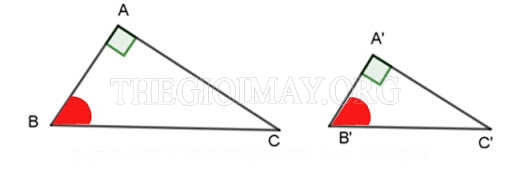
Nếu hai tam giác vuông có hai góc nhọn bằng nhau thì hai tam giác đó đồng dạng với nhau.
Điều này cũng khá dễ hiểu vì hai tam giác vuông này vốn dĩ đã có hai góc vuông bằng nhau trước đó rồi.
Chứng minh: Xét hai tam giác vuông ABC và tam giác A’B’C’, ta có:
Góc B = Góc B’
Góc A = Góc A’ = 90 độ
-> ∆ABC ∼ ∆A’B’C’ (dpcm)
Định lý đồng dạng phát biểu như thế nào?
Định lý Ta – lét có nội dung gì?
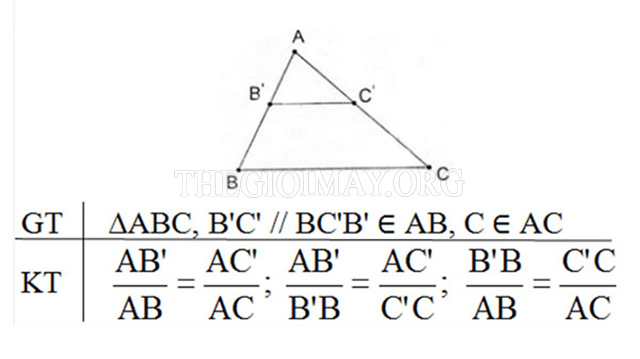
Theo nhà toán học Ta lét, nếu kẻ một đường thẳng đi qua một tam giác, cắt hai cạnh của tam giác đó đồng thời song song với cạnh còn lại thì nó sẽ tạo ra một tam giác mới đồng dạng với tam giác đã cho.
Định lý Talet đảo ra sao?
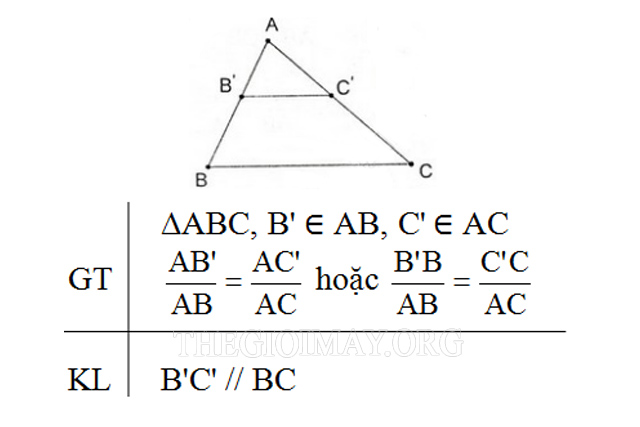
Định lý Talet đảo có nội dung như sau: Nếu một đường thẳng cắt hai cạnh của tam giác tại hai điểm và nó tạo ra những đoạn thẳng tương ứng tỉ lệ trên hai cạnh này thì đường thẳng đó song song với cạnh còn lại của tam giác.
Hệ quả của định lý Talet áp dụng cho trường hợp nào?
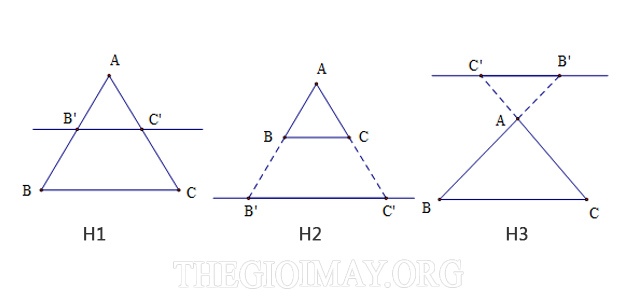
Hệ quả của định lý Talet phát biểu rằng: Nội dung của cả hai định lý Talet và Talet đảo đều sẽ đúng cho trường hợp đường thẳng song song với một cạnh và cắt đường thẳng kéo dài của hai cạnh còn lại trong tam giác.
Cụ thể, trong hình vẽ bên trên, ngoài trường hợp hình 1 ra thì hình 2 và hình 3 đều có thể áp dụng định lý Talet được.
Ta vẫn sẽ có tam giác ABC đồng dạng với tam giác A’B’C’ dù đường thẳng không trực tiếp cắt hai cạnh của tam giác mà chỉ cắt đường thẳng kéo dài của hai cạnh và tạo ra các cặp cạnh tỉ lệ.
Tính chất của 2 tam giác đồng dạng là gì?
- Tính chất giao hoán: Nếu tam giác ABC đồng dạng với tam giác A’B’C’ thì ngược lại, tam giác A’B’C’ cũng đồng dạng với tam giác ABC
- Tính chất bắc cầu: Nếu tam giác ABC đồng dạng với tam giác DEF. Mà tam giác DEF lại đồng dạng với tam giác HIK thì ta có thể suy ra rằng: Tam giác ABC đồng dạng với tam giác HIK.
Ngoài ra, hai tam giác đồng dạng còn có các tính chất như:
- Tỉ số diện tích của hai tam giác đồng dạng chính bằng bình phương của tỉ số đồng dạng.
- Tỉ số hai đường cao tương ứng bằng với tỷ số đồng dạng
- Tỉ số hai đường trung tuyến (Đường xuất phát từ một góc đi qua trung điểm của cạnh đối diện) cũng bằng tỷ số đồng dạng
- Tỉ số chu vi của hai tam giác bằng với tỷ số đồng dạng.
Nếu bạn chưa rõ tỷ số đồng dạng là gì thì nó chính là tỷ số của hai cặp cạnh trong tam giác đồng dạng đó. Ví dụ:
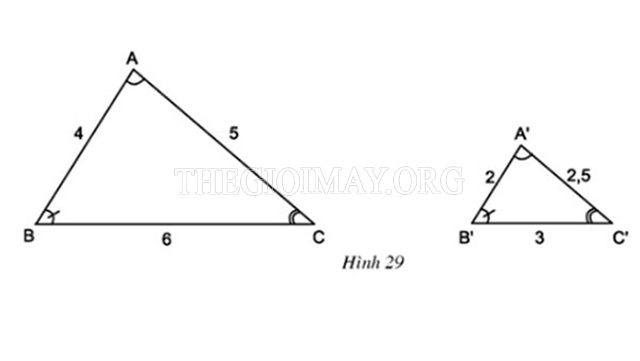
Ta có hai tam giác ABC và tam giác A’B’C’ (Như hình vẽ) là tam giác đồng dạng. Tỷ số đồng dạng của chúng sẽ là:
A’B’/AB = B’C’/BC = 1/2 (= 2/4 = 3/6).
Như vậy, tỉ lệ diện tích S∆A’B’C’/ S∆ABC =(1/2)^2=1/4.
Bạn lưu ý: Đường trung trực (Đường vuông góc tại trung điểm của một đoạn thẳng) không liên quan gì tới tam giác đồng dạng đâu nhé.
Lời kết
Trên đây là nội dung kiến thức cơ bản về tam giác đồng dạng mà thegioimay.org chia sẻ với bạn. Hy vọng rằng bạn sẽ nắm rõ được những khái niệm này để giành điểm cao trong bài kiểm tra Toán sắp tới nhé. Và đừng quên theo dõi website để cập nhật tin tức mới mẻ, thú vị đấy!