Trong phần kiến thức toán học đại số lớp 7 các bạn học sinh đã được làm quen với tập hợp số khá mới lạ, đó là số vô tỉ, số hữu tỉ thuộc tập hợp số thực. Tuy nhiên, chúng tôi nhận thấy rằng, đa phần các bạn học sinh vẫn hay bị nhầm lẫn giữa các tập hợp số vô tỉ, số hữu tỉ. Vì vậy trong bài viết này, hãy cùng chúng tôi tìm hiểu xem số vô tỉ, số hữu tỉ là gì, cách phân biệt số vô tỉ và số hữu tỉ đơn giản nhất nhé!

Nội dung chính
Số hữu tỉ là gì?
Số hữu tỉ là tập hợp tất cả các số có thể viết được dưới dạng phân số (thương số).
Nói cách khác, số hữu tỉ có thể được biểu diễn bằng một số thập phân vô hạn tuần hoàn.
Số hữu tỉ được viết dưới dạng thức là a/b, trong đó a và b là các số nguyên nhưng số b phải khác 0
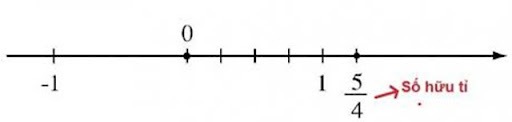
Tập hợp các số hữu tỉ được ký hiệu bằng chữ cái Q. Vậy ta có tập hợp Q các số hữu tỉ:
Q = {a/b; a, b ∈ Z, b≠0}
Tập hợp số hữu tỉ là tập hợp các số đếm được
Vậy, Căn 2 có phải là số hữu tỉ không? Câu trả lời là KHÔNG vì 2 không viết được dưới dạng thức a/b
Tính chất số hữu tỉ
- Tập hợp số hữu tỉ là tập hợp các số đếm được.
- Phép nhân số hữu tỉ có dạng a/b * c/d = a*c/ b*d
- Phép chia số hữu tỉ có dạng a/ b : c/d = a*d/ b*c
- Nếu số hữu tỉ là số hữu tỉ dương (+) thì số đối số đó sẽ là số hữu tỉ âm (-) và ngược lại. Tức là tống số hữu tỉ và số đối của nó bằng 0.
Lũy thừa của một số hữu tỉ
Lũy thừa của một số hữu tỉ bất kỳ được viết dưới dạng phân số
* Lũy thừa của một số hữu tỉ với số mũ tự nhiên
Khi viết số hữu tỉ x dưới dạng phân số ab, (a, b ∊ Z. b≠0), ta có:
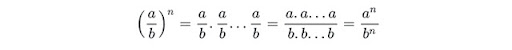
Do đó:
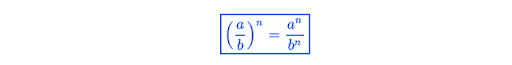
Ví dụ:
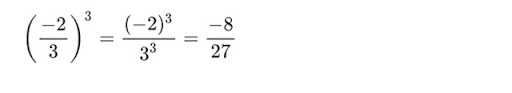
Các công thức lũy thừa của một số hữu tỉ tiếp theo:
- Thương và tích của hai lũy thừa cùng cơ số
- Lũy thừa của lũy thừa
- Lũy thừa của một tích
- Lũy thừa của một thương
Cộng trừ số hữu tỉ
* Quy tắc cộng trừ số hữu tỉ
Khi cộng, trừ số hữu tỉ chuyển một số hạng từ vế này sang vế kia của cùng một đẳng thức thì ta phải đổi dấu số hạng đó.
* Tính chất cộng trừ số hữu tỉ
- Phép cộng số hữu tỉ có đầy đủ các tính chất của phép cộng phân số:
- Tính chất giao hoán: x+y=y+x
- Tính chất kết hợp: (x+y)+z=x+(y+z)
- Cộng với số 0: x+0=x
- Mỗi số hữu tỉ bất kỳ đều có một số đối.
Giá trị tuyệt đối của một số hữu tỉ
Giá trị tuyệt đối của một số hữu tỉ x được kí hiệu là |x|, được tính bằng khoảng cách từ điểm x tới điểm O trên trục số.
- Nếu x > 0 thì |x| = x.
- Nếu x = 0 thì |x| = 0.
- Nếu x < 0 thì |x| = -x.
Từ định nghĩa về giá trị tuyệt đối của số hữu tỉ, ta có thể viết như sau:

Ví dụ:
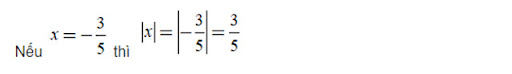
=> Nếu x = 6 thì |x| = |6| = 6.
Chú ý: Với mọi x ∈ Q ta luôn có |x| ≥ 0, |x| = |-x|, |x| > x
Số vô tỉ là gì?
Số vô tỉ là tập hợp các số có thể viết được dưới dạng số thập phân vô hạn không tuần hoàn.
Tập hợp số vô tỉ là tập hợp tất cả các số không đếm được.
Tập hợp số vô tỉ được kí hiệu là chữ cái I
Ví dụ:
Số √ 2 (căn 2)
Số thập phân vô hạn có chu kỳ thay đổi như: 0.1010010001000010000010000001…
Số = 1,41421 35623 04880 73095 16887 24209 7…
Số pi = 3,14159 26535 89793 26433 83279 50288 23846 41971 69399 37510 58209 74944…
Số logarit tự nhiên e = 2,71828 18284 59045 23536…
Sự khác nhau giữa số vô tỉ và số hữu tỉ
| Số vô tỉ | Số hữu tỉ | |
| Số thập phân | Vô hạn không tuần hoàn | Vô hạn tuần hoàn |
| Dạng số | Nhiều dạng | Phân số |
| Đếm được | Không | Có |
| Ký hiệu tập hợp | I | Q |
Số vô tỉ, Số hữu tỉ, Số thực có mối quan hệ gì?
Định nghĩa số thực
Số thực là tập hợp bao gồm số dương(1,2,3), số âm(-1,-2,-3), số 0, số hữu tỉ (5/2, -2/5), số vô tỉ (số pi, số √ 2).
Số thực có thể được xem là các điểm thuộc trục số dài vô hạn. Nói cách đơn giản hơn thì số thực là tập hợp các số hữu tỉ và số vô tỉ.
Tập hợp số thực kí hiệu là chữ R (R = Q, U, I).
Ngoài ra, một số thực có thể là số đại số hoặc là số siêu việt. Ta cũng có số thực âm (-2, -3/4…) và số thực dương (3, 7, √ 2…).
Số hữu tỉ và số vô tỉ được gọi chung là các số thực. Kí hiệu: R
Nếu a là số thực thì a có thể biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn.
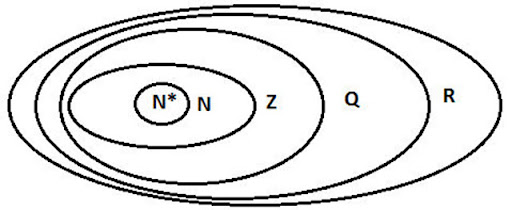
Mối quan hệ các tập hợp số
Ký hiệu các tập hợp số:
- N: Tập hợp số tự nhiên
- N*: Tập hợp số tự nhiên khác 0
- Z: Tập hợp số nguyên
- Q: Tập hợp số hữu tỉ
- I: Tập hợp số vô tỉ
Ta có : R = Q ∪ I.
Tập N ; Z ; Q ; R.
Khi đó, quan hệ bao hàm giữa các tập hợp số sẽ là : N ⊂ Z ⊂ Q ⊂ R
>>> Bài viết tham khảo: Shout Out Là Gì? Ghi Nhớ Ngay Những Cấu Trúc Liên Quan Đến “Shout Out”
Vậy là bài viết đã cung cấp cho các bạn học sinh kiến thức bổ ích về số vô tỉ, số hữu tỉ, cách phân biệt các tập hợp số này cùng mối quan hệ giữa chúng. Hy vọng bài viết đã truyền cảm hứng học môn Toán cho những bạn còn đang sợ hay lười học Toán sẽ tích cực và yêu thích môn Toán hơn vì đây thực sự là môn học bổ ích.




