Trong phần hình học của chương trình toán 4 và toán 8, hình thoi là một kiến thức quan trọng, xuất hiện nhiều trong bài kiểm tra. Vậy hình thoi là gì? Công thức tính hình thoi và dấu hiệu nhận biết ra sao? Mời bạn hãy theo dõi nội dung chi tiết dưới đây của thegioimay.org nhé!
Nội dung chính
Hình thoi là gì? Có phải là hình bình hành đặc biệt?
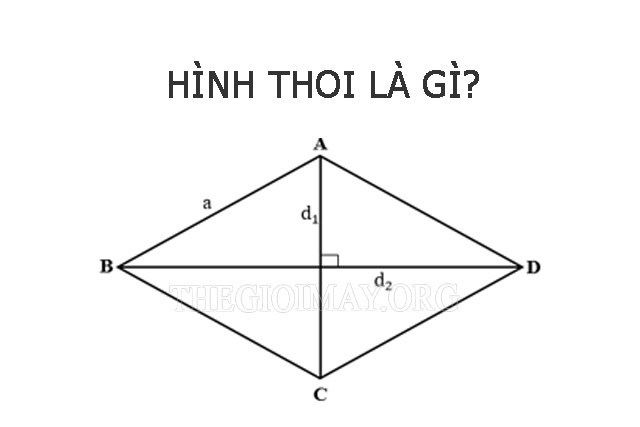
Hình thoi là một tứ giác sở hữu 4 cạnh có độ dài bằng nhau. Nó cũng là một hình bình hành đặc biệt có hai cạnh kề bằng nhau và hai đường chéo vuông góc với nhau.
Hình thoi có dấu hiệu nhận biết như thế nào?

Trong các bài tập toán hình học, có không ít bài đưa ra yêu cầu: Chứng minh một tứ giác là hình thoi. Vì vậy, bạn cần nắm rõ các dấu hiệu nhận biết sau đây để có thể “giải quyết” bài toán nhanh chóng:
*Dấu hiệu nhận biết tứ giác là hình thoi gồm những gì?
- Một tứ giác có 4 cạnh bằng nhau thì đó chính là hình thoi
- Tứ giác có hai đường chéo cắt nhau và là đường trung trực của nhau thì là hình thoi
- Tứ giác sở hữu 2 đường chéo đồng thời là đường phân giác của 4 góc thì đó là hình thoi.
*Dấu hiệu nhận biết hình bình hành là một hình thoi
Chúng ta đã biết, hình thoi là một hình bình hành đặc biệt. Vì vậy chỉ cần một hình là hình bình hành và có thêm các đặc điểm sau đây thì chúng sẽ được coi là hình thoi:
- Hai cạnh kề bên có độ dài bằng nhau
- Có hai đường chéo cắt nhau và vuông góc với nhau.
- Có một đường chéo là đường phân giác của một góc bất kì.
Hình thoi có những tính chất nào?
Hình thoi sẽ có những tính chất dưới đây:
- Trong một hình thoi, chúng ta sẽ có 2 cặp góc vừa đối đối nhau, vừa bằng nhau.
- Hai đường chéo của hình thoi cắt nhau, vuông góc với nhau tại đúng trung điểm của mỗi đường (Có thể coi là đường trung trực luôn).
- Hai đường chéo chính là hai đường phân giác của 4 góc trong hình thoi.
- Vì là một hình bình hành đặc biệt nên hình thoi vẫn sở hữu tất cả các tính chất của hình bình hành. Ví dụ như: Có 2 cặp cạnh song song với nhau.
Diện tích hình thoi – Những cách tính đơn giản

*Tính diện tích hình thoi dựa vào độ dài của hai đường chéo
Diện tích hình thoi sẽ bằng một nửa tích độ dài của hai đường chéo. Công thức cụ thể như sau: S= 1/2 x d1 x d2
Trong đó, d1, d2 lần lượt là độ dài của hai đường chéo trong hình thoi.
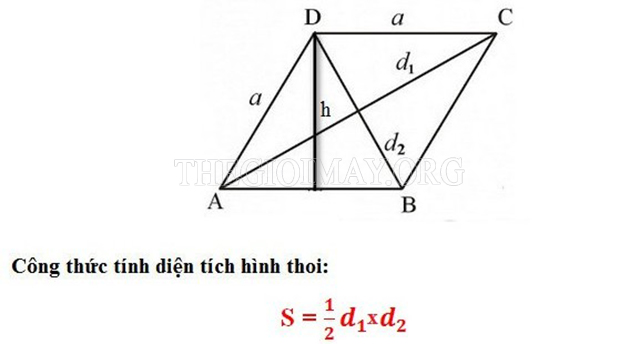
Ví dụ: Hình thoi ABCD có độ dài hai đường chéo lần lượt là 10cm và 6cm, hãy tính diện tích hình thoi: S hình thoi = (10 x 6) : 2 = 30cm2
*Tính diện tích hình thoi dựa vào độ dài đáy và chiều cao
Diện tích hình thoi sẽ bằng tích độ dài của đáy và chiều cao a: S hình thoi = h x a. Trong đó, a là độ dài cạnh (Cạnh đáy), h là chiều cao của hình.
Ví dụ: Cho hình thoi IEDF có độ dài cạnh là 7cm, chiều cao 4cm. Tính diện tích hình thoi này.
Giải: S hình thoi = h x a = 4 x 7 = 28 cm2.
Bạn hãy nhớ để đơn vị diện tích là xăng – ti – mét vuông nhé để tránh bị trừ điểm trình bày.
*Tính dựa vào hệ thức trong tam giác, dùng hàm sin
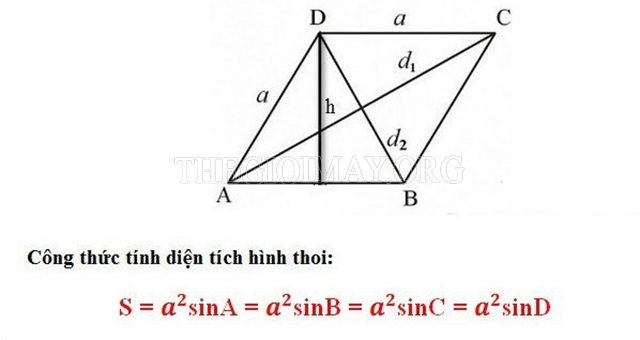
Ngoài hai cách tính diện tích hình thoi cơ bản trên, bạn cũng có thể tham khảo cách tính sau nếu biết số đo của các góc trong hình:
S thoi = a2 x sin A = a2 X sin B = a2 x sin C = a2 x sinD
Trong đó, a là độ dài của một cạnh (Vốn dĩ 4 cạnh trong hình thoi đều bằng nhau nên chúng ta chỉ cần độ dài của một cạnh là đủ rồi).
Tính chu vi hình thoi thế nào?

Cách tính chu vi hình thoi rất đơn giản, bạn chỉ cần cộng số đo của các cạnh lại. Tuy nhiên, vì hình thoi có 4 cạnh đều bằng nhau nên bạn hãy lấy độ dài a của một cạnh nhân với 4: P = a x 4. (Với p là chu vi hình thoi, còn a là độ dài của 1 cạnh trong hình thoi).
Ví dụ: Cho hình thoi EFGH có độ dài một cạnh là 5cm, tính chu vi hình thoi đó.
Lời giải: Chi vi hình thoi là: P hình thoi = 5 x 4 = 20cm.
Lời kết
Đọc đến đây, chắc hẳn bạn đã nắm rõ khái niệm hình thoi là gì và dấu hiệu nhận biết, công thức tính diện tích của hình này rồi đúng không nào? Hy vọng rằng bạn sẽ ghi nhớ được kiến thức và giành điểm 9, 10 trong bài kiểm tra trên lớp nhé! Hẹn gặp lại bạn ở các bài viết lần sau của thegioimay.org!




