Hình chóp là một nội dung quen thuộc trong chương trình hình học không gian ở bậc Phổ thông. Vậy hình chóp là gì, hình chóp có những loại nào và cách tính diện tích, chu vi, thể tích của nó ra sao? Mời bạn theo doĩ bài viết sau đây của thegioimay.org để biết câu trả lời nhé!
Nội dung chính
Hình chóp là gì?

Hình chóp là một loại hình học không gian có mặt đáy là đa giác lồi còn các mặt bên là tam giác có cùng chung một đỉnh. Đỉnh này cũng chính là đỉnh của hình chóp.
Có rất nhiều loại hình chóp khác nhau, sự khác biệt chủ yếu là hình dạng của đa giác dưới đáy hoặc số mặt. Người ta cũng sử dụng các đặc điểm này để gọi tên hình chóp.
Ví dụ: Hình chóp có 4 mặt người ta gọi là tứ diện. Còn hình chóp có đáy là tam giác người ta gọi là hình chóp tam giác, hình chóp có đáy là tứ giác thì sẽ được gọi là hình chóp tứ giác.
Tính chất nổi bật của hình chóp là gì?

Hình chóp sẽ sở hữu một số tính chất nổi bật sau đây:
- Đường cao của hình chóp chính là một đường thẳng đi qua đỉnh và vuông góc với mặt đáy.
- Nếu một hình chóp có các cạnh bên hợp với mặt phẳng đáy các góc bằng nhau thì chân đường cao của hình chóp chính là tâm đường tròn ngoại tiếp của mặt đáy.
- Nếu hình chóp có các mặt bên hợp với mặt đáy một góc bằng nhau hoặc hình chóp có các đường cao của mặt bên cùng xuất phát từ một đỉnh bằng nhau thì chân đường cao sẽ là tâm đường tròn nội tiếp của đa giác mặt đáy.
- Hình chóp có các mặt bên hoặc mặt chéo vuông góc với mặt phẳng đáy thì đường cao của hình chóp cũng chính là đường cao của mặt phẳng bên hoặc mặt chéo.
Có những loại hình chóp thường gặp nào?
Dưới đây là những hình chóp mà chúng ta thường gặp trong các bài toán:
| Tên hình chóp | Hình dạng đáy | Mặt bên | Số cạnh của đáy | Số mặt hình chóp | Số cạnh bên |
| Hình chóp tam giác đều | Tam giác đều | Tam giác đều | 3 | 4 | 6 |
| Hình chóp tứ giác đều | Hình vuông | Tam giác cân | 4 | 5 | 8 |
| Hình chóp ngũ giác đều | Ngũ giác đều | Tam giác cân | 5 | 6 | 10 |
| Hình chóp lục giác đều | Lục giác đều | Tam giác cân | 6 | 7 | 12 |
Bảng tóm tắt những dạng hình chóp thường gặp
Hình chóp tam giác đều – Tính chất cơ bản
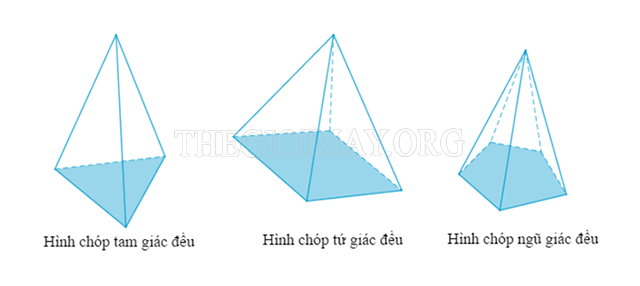
Hình chóp tam giác đều là hình chóp có mặt đáy là một tam giác đều, còn các mặt bên của nó là các tam giác cân có chung đỉnh.
Hình chóp tam giác đều sở hữu một vài tính chất nổi bật sau đây:
- Hình chóp tam giác đều có tất cả 3 mặt phẳng đối xứng
- Tất cả các cạnh bên của hình chóp tam giác đều đều bằng nhau.
- Chân đường cao của nó trùng với tâm của mặt đáy
- Tất cả các góc tạo bởi mặt bên và mặt đáy của hình chóp tam giác đều đều bằng nhau.
- Các góc tạo bởi cạnh bên và mặt đáy của hình chóp tam giác đều cũng bằng nhau.
Hình chóp tứ giác đều – Tính chất cơ bản
Hình chóp tứ giác đều là hình chóp có mặt đáy là một hình vuông, còn các mặt bên của nó đều là tam giác cân có cùng chung một đỉnh (Chính là đỉnh của hình chóp).
Dưới đây là một vài tính chất cơ bản của hình chóp tứ giác đều:
- Tất cả các cạnh bên của hình chóp tứ giác đều đều bằng nhau.
- Chân đường cao của hình chóp trùng với tâm của mặt đáy
- Tất cả các góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều đều bằng nhau
- Hình chóp tứ giác đều có 8 cạnh tất cả.
Hình chóp cụt đều là gì? Tính chất
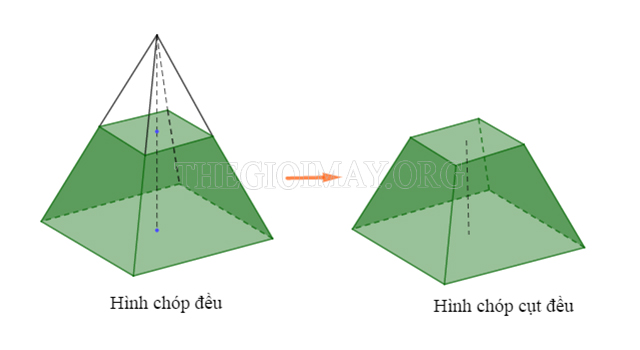
Hình chóp cụt đều là hình chóp bị cắt bởi một mặt phẳng song song với mặt đáy.
Tính chất cơ bản của hình chóp cụt đều là:
- Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
- Hình chóp cụt đều có tới 2 mặt đáy, mặt đáy ở dưới sẽ lớn hơn mặt đáy ở trên.
- Hai mặt đáy trên và đáy dưới này song song với nhau.
- Hai đáy là hai đa giác đều có cạnh tương ứng song song và tỉ số các cạnh tương ứng bằng nhau.
- Những đường thẳng chứa cạnh bên sẽ đồng quy tại một điểm.
Công thức tính chu vi, diện tích, thể tích của hình chóp ngắn gọn
- Công thức tính chu vi hình chóp: Chu vi của một hình chóp sẽ bằng tổng chu vi của mặt đáy và mặt bên: P = P đáy + P mặt bên
- Công thức tính diện tích xung quanh của hình chóp (Áp dụng với hình chóp tam giác và hình chóp tứ giác): Diện tích xung quanh của hình chóp đều sẽ bằng tích của nửa chu vi đáy với trung đoạn: Sxq=p.d
Trong đó trung đoạn là đường cao xuất phát từ đỉnh tới trung điểm của 1 cạnh.
- Công thức tính diện tích toàn phần của hình chóp sẽ bằng diện tích xung quanh cộng với diện tích đáy của hình chóp đó.
- Công thức tính thể tích của hình chóp: Thể tích hình chóp bằng một phần ba tích độ dài của chiều cao và diện tích đáy hình chóp: V=1/3.S.h
Trong đó: S là diện tích của mặt đáy hình chóp. Còn h là chiều cao của hình chóp.
Có thể bạn quan tâm:
Lời kết
Hy vọng rằng những chia sẻ của thegioimay.org về hình chóp là gì, tính chất của hình chóp đều đã giúp bạn nhớ lại và hệ thống hóa kiến thức đã được học. Để thường xuyên cập nhật các bài viết khác thú vị hơn, bạn hãy nhớ truy cập vào website của chúng tôi nhé!




